The true nature of the trading edge in quantitative finance

Professor Tommaso Gastaldi at "Sapienza" University, Rome offers a non-technical exploration of the role of “historical trading information”

A paper by Prof. T. Gastaldi recently published on ArXiv discusses the real nature of the edge in financial trading. The study proves that a source of a systematic long-term edge is represented by the so-called historical trading information (HTI) generated by a trading strategy.

This result contrasts with the more naive idea of extracting information from market data (such as prices, volumes, etc.) to gain an edge. This is a notion that is tacitly implied when using predictive models, pattern recognition, AI, etc. Aside from backtesting experiments (which are susceptible curve fitting and other types of logical fallacies), it has never demonstrated statistical significance in forward trading in a transparent and verifiable scientific context.

An anonymous referee of the QFE journal reviewed the paper using these words:

The manuscript "On a fundamental statistical edge principle" provides a significant contribution to the field of quantitative finance by presenting a thorough theoretical framework for enhancing trading strategies through the use of self-generated historical trading information (HTI). The authors argue convincingly that leveraging HTI is a necessary condition for establishing a statistical edge in trading practices.

The introduction lays a strong foundation by establishing the importance of HTI in constructing profitable trading strategies and setting the stage for the ensuing discussions. The paper proceeds to establish a theoretical basis for why any trading strategy that does not use its own HTI is inherently suboptimal, and how a strategy that does exploit HTI can consistently outperform it.

Moreover, the paper does well to address the real-world implications of the proposed principles, suggesting how these can be applied in actual trading scenarios and highlighting the potential for developing more sophisticated trading strategies that are in tune with the mechanics of financial instruments.

The authors have clearly identified the relevance of their research by not only focusing on the theoretical model but also discussing its practical applications in the real world and future lines of research, thus presenting a comprehensive view of its utility […]

It successfully bridges the gap between theoretical models and practical trading strategies, making it a valuable read for both academics and practitioners in the field of finance. I am impressed by the research contribution […]”

The study implies an epochal paradigm shift in the world of quantitative finance (for both theory and practice) concerning the real sources of a systematic long-term trading edge. Here we explain its novelty in purely intuitive terms, without using formulas and mathematical proofs, and explain the reason why this represents an iconoclastic breakthrough compared to the currently prevailing trading approaches.

Let’s start with the simplest example we can imagine. Consider a completely novice and naive practitioner who takes his first steps in the trading world, beginning with buying and selling a financial instrument, with the goal of obtaining a systematic long-term profit. For example, you can imagine a stock, an ETF, a futures contract, an option, etc.

He initiates his trading practice using some basic, naive trading “rules”. For example, he might buy a certain stock when some conditions that he deems relevant occur and sell it when certain other conditions are met. Let’s imagine that a first test strategy is to always buy the same quantity, for example, n shares, of the stock if there is a decline of d% and then sell it if there is either a price decline of s% or a price increase of p%.

Now, by applying these banal rules, which nevertheless define a deterministic "strategy", over time a sequence of orders will be generated with their matching close order, thus creating a sequence of trades.

Note that I am using this simple example with non-overlapping trades, only for the sake of example, since trading algorithms, apart from naive exceptions, implement more complex ideas that involve modulation of the position and exposure, and therefore the concept of a single "trade" is not used, and the matching of the traded lots is arbitrary.

As the novice trader advances his knowledge, he will want to introduce increasingly professional-looking rules to decide when to open and close a trade at a profit or loss. For example, imitating what he sees others doing, he might resort to technical analysis indicators (moving averages, oscillators, bands, etc.) or rely on predictive models, pattern recognition, AI, or any other form of market data analysis.

Furthermore, he will also certainly learn about backtesting, that is, simulating how the strategy would have performed on historical market data. This will naturally lead him to create ad hoc rules to generate the best possible results based on such data. This often results in “curve fitting” or “look-ahead bias” in the case of high-frequency strategies (that is, in the presence of trades too short relative to the indicators’ timeframe).

Regardless of the rules adopted, the strategy always generates a random sequence of trades, with some “winners” and “losers”. By aggregating the corresponding outcomes, a profit-and-loss (PnL) curve emerges over time, displaying fluctuations and possibly a long-term positive or negative drift. The trader aims for a long-term positive drift and, as he better understands the role of risk management, also to the minimisation of PnL oscillations, since very large negative fluctuations can lead to losses due to a lack of funds or increasing margin requirements.

Let’s consider the real-time evolution of the trades. When our practitioner initiates a new trade, he will do so when the conditions envisioned for a new entry are met. The universal statistical edge (USE) principle that is proved in the paper tells us that, whatever the rules used to trigger each new order, if they do not also take into account, in probabilistic terms, the historical trading information (HTI) generated by the strategy itself, the trader’s strategy will always be "inadmissible".

This is true in the technical sense because it can be proved mathematically that, for another trader who trades along and observes the trades, it will always be possible to build a new "dominant" strategy (taking advantage of the HTI and recurrence properties of the instrument’s price), such that the PnL difference between the second trader and the first tends to infinity.

This result could, at first glance, appear amazing because practically no one, in the current algorithmic trading landscape, has ever addressed the necessity to explicitly integrate the HTI into the process of formulating new orders. On the contrary, it is a ubiquitous but fallacious belief that it is possible to “learn” and extrapolate a systematic long-term edge from market data using, for example, predictive models or pattern analysis.

In recent times, with the massive hype about so-called AI, authoritative criticisms have arisen. Jim Covello (Head of Global Equity Research at Goldman Sachs) raised this in a recent interview, saying: “Not one transformative application [of AI] has been found.” 

A widespread belief, often perpetuated without much reflection, is that market data somehow contains encoded information that can be learned, and which can provide signals for a systematic probabilistic advantage. This is a transfer of concepts from signal theory and processing or statistical inference that work well in other contexts, such as engineering and physics.

However, from a conceptual point of view, they do not appear to have relevance in financial trading, where there are no real “underlying laws” or significant regularities to be exploited, neither deterministic nor probabilistic.

Therefore, the naively appealing idea that “learning” from market data can generate a long-term systematic edge lacks a foundation or statistical validity and is arguably a form of apophenia or even “magical thinking”, typical cognitive biases that still plague the world of financial trading: "the belief that unrelated events are causally connected despite the absence of any plausible causal link between them". 

This appears even more rationally implausible if we think about the actual mechanisms behind the generation of bid/ask prices and traded volumes: namely, the activity of market-making (mm) algorithms in the exchanges. It is naive to assume that such algorithms would generate information from which one can learn, when their main goal, having fulfilled the institutional obligation of execution and supply of liquidity, is to maximise their payoff, primarily based on the flow of incoming orders and on the appropriate formulation of the price using the available volume.

On the contrary, if any conspiratorial hypothesis had ever to be made about possible signals provided by a market-making algorithm and its real-world implementation, it would rather be of adversarial or confounding nature.

The theorem proved in the paper highlights the true nature of the edge in trading, which is essentially generated by information. Not information to be “learned” or decoded from market data, but information self-generated during the trading process. This ensures inner consistency of the long-term trading outcome and contributes to building up a positive drift. In other words, a necessary condition for any strategy not to be immediately dominated and therefore to be admissible is that it makes use of such self-generated HTI.

This result represents a historical breakthrough in quantitative finance because it explicitly highlights that the true source of the edge in trading applications is not coming from market data but is rather the result of an accumulation of information that is generated by the trading strategy itself, along with some intrinsic characteristics of the market such as, for example, the recurrence of prices (randomly occurring in the time series of prices, or induced via folio management, for particular financial instruments where this is possible).

This universal statistical edge principle also hints at how immaterial the discussion about the EMH is, for the purpose of systematic profitability, as well as the opposing theories of behavioural finance, which all remain unfalsifiable beliefs and, therefore, essentially irrelevant in real-world applications, while, at the same time, providing rigorous mathematical proof of what can contribute to the edge. In this sense, realised financial losses are, in intuitive terms (not referring here to the accounting meaning), essentially the result of the destruction or disregard of such information.

In this short note, I glided over math proofs to indulge in the main ideas and provide a philosophical and conceptual framework along with some intuitive interpretation that can help identify the implications for the theory and practice of quantitative finance. Please refer to the original article for more details and also additional considerations about the importance of risk management to effectively use your edge. 

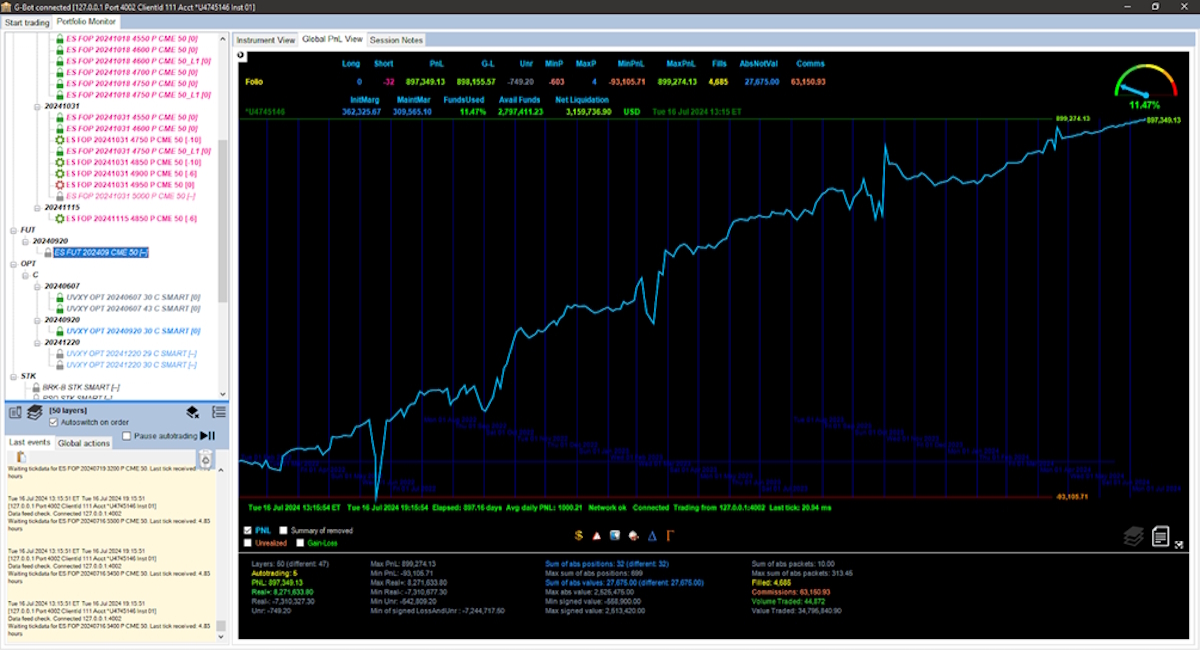
Finally, note that the relevance of the discussed principle is not purely philosophical but, on the contrary originally stemmed from an attempt to formalise a phenomenon observed in extensive real-world applications. The seminal paper also contains (page 9) a pointer to real long-term trading results obtained through a specific implementation of the USE principle mentioned here. 

For example, the screenshot below (Figure 1) shows actual results and PnL drift over approximately 2 years (initial funds: 2MM), and it is also apparent the positive drift induced in the PnL curve by the use of information (HTI) and the price recurrence properties (in this specific case, induced through appropriate portfolio management).